Floating Point Numbers

Floating Point Numbers A hands-on approach

Back to the main page

Writing a simple calculation like 5.6 * 4.7 on a computer seems simple. But in order to have it perform mathematical calculations using decimal numbers you have to use floating point numbers. IEEE 754 is a standard for floating point numbers. (IEEE stands for Institute of Electrical and Electronics Engineers)
Floating point numbers are usually represented in the form
x = ± m × re
where
m is the mantissa
e is the exponent
r is the base

usually 1 > m ≥ r-1

Physically it looks like this:
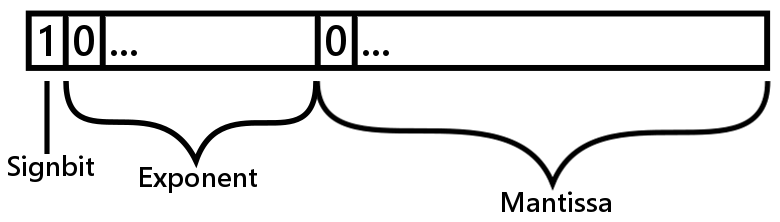
Bitmap Floating Point Number
According to the IEEE 754 standard a single precision floating point number is 4 bytes. It has one sign bit. The exponent is 8 bits and the mantissa is 23 bits.
A double precision number is 8 bytes long. It still has one sign bit but the exponent is 11 bits and the mantissa is 52 bits long.

If x and y are floating point numbers it's usually no good to test in code whether x and y are equal like this:
if (x == y)
{
    i = 123;
}

You may think you have 4.7 in the variable x and 4.7 in y. Now you want to test whether the two are equal. Because of the binary nature of the representation it's not possible to represent 4.7 exactly. For a computer to accomplish this, the mantissa would need to have an infinite number of bits. No physical computer has an infinite number of bits. So it's impossible! Therefore the people who designed the computer made a compromise. They settled for approximately representing 4.7 instead of representing it exactly. This will mean that in the variable x you have 4.7FFFFFFFFFFFF001 and in y you have 4.6999999999999999. Are these two equal? No they're not! Therefor it's better to test whether x and y are approximately equal like this:

if (ABS(x - y) < 0.000001)
{
    i = 123;
}

Converting a decimal number into a floating point binary number
Example of converting 754.7 into an IEEE 754 single precision floating point number:
Prerequisites: The remainder when performing integer division between two numbers is called the modulus of these two numbers. This is denoted as x % y in C# or Java. I will denote integer division using the / symbol.
Thus: 3 / 2 = 1;
9 % 5 = 4;
Converting a decimal number into an IEEE 754 floating point number can be accomplished using the algorithm described below:
You start with the integer part of 754.7, which is 754.
  1. 754 % 2 = 0
  2. 754 / 2 = 377. 377 % 2 = 1
  3. 377 / 2 = 188. 188 % 2 = 0
  4. 188 / 2 = 94. 94 % 2 = 0
  5. 94 / 2 = 47. 47 % 2 = 1
  6. 47 / 2 = 23. 23 % 2 = 1
  7. 23 / 2 = 11. 11 % 2 = 1
  8. 11 / 2 = 5. 5 % 2 = 1
  9. 5 / 2 = 2. 2 % 2 = 0
  10. 2 / 2 = 1. 1 % 2 = 1
Counting from the bottom to the top the rightmost numbers become the binary number 1011110010

The decimal numeral system works like this:
754 = 7 * 102 + 5 * 101 + 4 * 10 0
The binary numeral system works exactly the same way. But instead of using powers of ten you now use powers of two like this:
1 * 22 + 0 * 21 + 1 * 20 = 5
So 101 in binary form is 5 in decimal form (base ten).
Let's see if we were right! Is 1011110010 = 754?
1 * 29 + 0 * 28 + 1 * 27 + 1 * 26 1 * 25 + 1 * 24 + 0 * 23 0 * 22 + 1 * 21 + 0 * 20
=
1 * 512 + 0 * 256 + 1 * 128 + 1 * 64 + 1 * 32 + 1 * 16 + 0 * 8 + 0 * 4 + 1 * 2 + 0 * 1
= 754
Correct!

Now for the decimals:
The fractional part of 754.7 is 0.7.
  1. 0.7 * 2 = 1.4 keep the digit in front of the decimal place, which is 1
  2. Now discard the 1 in 1.4. All leftmost numbers have to be less than 1
  3. 0.4 * 2 = 0.8 keep the 0
  4. 0.8 * 2 = 1.6 keep the 1
  5. 0.6 * 2 = 1.2 keep the 1
  6. 0.2 * 2 = 0.4 keep the 0
  7. 0.4 * 2 = 0.8 keep the 0
  8. 0.8 * 2 = 1.6 keep the 1
  9. 0.6 * 2 = 1.2 keep the 1
  10. 0.2 * 2 = 0.4 keep the 0
  11. 0.4 * 2 = 0.8 keep the 0
  12. 0.8 * 2 = 1.6 keep the 1
This keeps repeating over and over and over again. Like this (counting from the top towards the bottom this time)

0.7 = 10110011001100110011001100110011001100110011001100110011001100110011001100...

The binary numeral system for numbers < 1.0 uses negative powers of two instead of positive. Like this:
1 * 2-1 + 0 * 2-2 + 1 * 2-3 + 1 * 2-4
So 0.1011 in binary form is 0.6875 using the decimal numeral system (base ten):
1 * 0.5 + 0 * 0.25 + 1 * 0.125 + 1 * 0.0625 = 0.6875

Using what we have gained so far 754.7 now becomes
1011110010.101100110011001100110011001100110011...
Transform this into scientific notation. The decimal point has to be shifted 9 steps to the left. You get 1.011110010101100110011001100110011001100110011... × 29.
To be able to use both negative and positive exponents IEEE 754 has specified a bias for the exponent. This bias is 127. Add to 127 the number of times we shifted the decimal point to the left in the step above. 127 + 9 = 136. If we would have shifted it to the right it would have been 127 - 9 = 118. Now convert 136 into a binary number:
  1. 136 % 2 = 0
  2. 136 / 2 = 68. 68 % 2 = 0
  3. 68 / 2 = 34. 34 % 2 = 0
  4. 34 / 2 = 17. 17 % 2 = 1
  5. 17 / 2 = 8. 8 % 2 = 0
  6. 8 / 2 = 4. 4 % 2 = 0
  7. 4 / 2 = 2. 2 % 2 = 0
  8. 2 / 2 = 1. 1 % 2 = 1
In other words 10001000 which is our 8-bit exponent. (from the bottom to the top again)
Our mantissa is the first 23 bits of the digits after the decimal place in our scientific notation of 754.7, which was 1.011110010101100110011001100110011001100110011...
So it's
011110010101100110011001100110011001100110011...
Using this to compile the IEEE 754 representation of 754.7 gives us:
Sign bit: 0 for positive, 1 for negative (754.7 is positive so in our case it's 0) Exponent: 10001000
Mantissa: 01111001010110011001100

Most floating point systems uses rounding instead of chopping. If you preferr chopping, the mantissa 01111001010110011001100 would be correct. But IEEE 754 uses rounding. The part of the mantissa which was cut off started 110011001100110011001100...
The first digit is the only one to be taken into account. Just like when you round 1.7 to 2.0, 1-4 is rounded downwards and 5-9 is rounded upwards. In the binary case 01 is rounded upwards to 10 and 00 is rounded downwards to, well, 00.
So the
     Mantissa: 011110010101100110011001
is rounded to: 01111001010110011001101

Putting the sign bit, exponent and mantissa together it becomes 0 10001000 01111001010110011001101
or
01000100001111001010110011001101

DONE!